iamk Inhalte – iamk GmbH

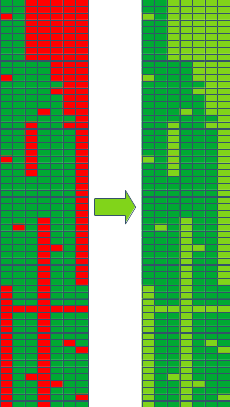
Das Füllen von Lücken in Zeitreihen (zur Motivation hier entlang) hat eine Menge Anforderungen an die Methodik:

Einerseits soll die Qualität der Lückenfüllung natürlich hoch sein, d. h. die gefüllten Werte einer Zeitreihe sollen möglichst nah an den tatsächlich aufgetretenen, aber nicht gemessenen Werten liegen. Das mag trivial klingen, jedoch gibt es einige einfache Methoden, wo beispielsweise bei Temperaturzeitreihen die Lücken mit Jahresmittelwerten ersetzt werden. Damit bleib der Mittelwert der Zeitreihe erhalten, die Werte zu den einzelnen Zeitpunkten sind jedoch grob fehlerhaft.

Als nächstes sollte die Methodik damit zurechtkommen, die Lücken sowohl mit wenigen, als auch mit vielen Stützstellen schließen zu können. Stellen wir uns eine Zeitreihe vor, die seit 20 Jahren misst, und wir wollen diese auf eine Länge von 100 Jahre erweitern (ja, das geht 🙂). Zu Beginn des 20. Jhd. gab es nur relativ wenige Messstationen, die als Stützstelle verwendet werden könnten. In den letzten 50 Jahren hingegen ist die Anzahl der Messstationen stark gestiegen. Nun wollen wir sowohl für die weitere als auch die nähere Vergangenheit soviel Informationen (d.h. Stützstellen) verwenden, wie nur irgend möglich, um die bestmögliche Qualität der Lückenfüllung zu erreichen.

Nun ist es so, dass die Zeitreihen, die zur Füllung der Lücken an einer bestimmten Station als Stützstellen verwendet werden sollen, selbst auch Lücken aufweisen. Das bedeutet, dass die Methode mit Lücken in den Stützstellen umgehen können muss. Die allermeisten Methoden können das nicht, so dass die Lücken in den Stützstellen selbst erst mit einer sehr einfachen Methode gefüllt werden müssen, oder die Anzahl der Stützstellen wird drastisch reduziert. Eine weitere Möglichkeit wäre, für jede Lücken eine eigene Liste mit Stützstellen zu erstellen. All dies führt entweder zu einer sehr hohen Rechenzeit oder zu größeren Ungenauigkeit in der Berechnung.

Nicht zuletzt soll die Rechenzeit natürlich erträglich sein. Wenn man für einige Jahrzehnte Stundenwerte meteorologischer Größen aller Stationen in Deutschland rechnet, so kommen einige Hunderttausend Zeitpunkte bei einigen Tausend Zeitreihen heraus. Und jede dieser Zeitreihen hat wieder für sich einige Hundert Zeitreihen als Stützstellen.

Die Methode der Wahl fällt hier auf „Gradient Boosting“, genauer „Gradient Boosted Decision Trees“. Wie der Name sagt, werden hier mit Methoden des maschinellen Lernens Entscheidungsbäume erstellt. Diese bilden die Eigenschaften der Zielgröße, also beispielsweise des Niederschlages an einer bestimmten Stationen, in Abhängigkeit von verschiedenen Stützstellen ab. Diese Stützstellen sind Niederschlagszeitreihen anderer Stationen, aber auch andere Zeitreihen wie die Temperatur, Feuchte, Windgeschwindigkeit oder das Datum gehen in die Entscheidungsbäume mit ein. Der Zusammenhang ist nicht parametrisch und nicht linear, es werden für ein Abbild einige Hundert Bäume mit bis zu zehn Ebenen verwendet.

Die Verwendung von Gradient Boosting löst einige Probleme bereits: Die Berechnung erfolgt extrem schnell, da sie auf Grafikkarten ausführbar ist. Da man mehr Zeitreihen in der gleichen Zeit füllen kann, kann so eine Aufgabe natürlich trotzdem einige Zeit dauern. Die Methodik erlaubt es außerdem, Lücken in den Stützstellen zu verwenden.

Als nächstes sollte Gradient Boosting gleichzeitig mit vielen als auch wenigen Stützstellen zurechtkommen. Das ist nicht grundsätzlich gegeben, hier muss an den zahlreichen Parametern geschraubt werden, um diesen Zustand zu erreichen. Wir nutzen zur Parameteroptimierung eine Kreuzvalidierung mittels genetischem Lernen.

Um aber wirklich gut zu sein braucht es noch etwas mehr. Die Anforderungen sind vielfältig: Die Einzelwerte sollen möglichst gut getroffen werden. Die Statistik der gesamten Zeitreihe soll erhalten werden. Es soll möglich sein, kurze Lücken, vielleicht nur eine Stunde lang, ebenso zu füllen, wie eine Zeitreihe um 100 Jahre in die Vergangenheit zu verlängern. Für all das haben wir ein Framework um die Gradient Boosting Methode herum entwickelt. Das umfasst neben einigen anderen auch state of the art-Methoden wie blending und bagging ebenso wie das Clustern der Lücken, um möglichst effektiv Subzeiträume für die Lückenfüllung zu bestimmen. Mit welcher Qualität bei den unterschiedlichen Szenarien zu rechnen ist, zeigt in Kürze ein anderer Blogpost. Eine Übersicht zur erwarteten Qualität bei einzelnen Lücken gibt es hier in meinem Paper von 2018.

Schematische Darstellung der Lückenfüllung: Links sieben Zeitreihen mit Messdaten (dunkelgrün) und Lücken (rot). Rechts sind die Lücken aller Zeitreihen gefüllt (hellgrün)

Tl;dnr
Grund die Firma zu gründen war es, einen Service anbieten zu können, den ich selbst gern des öfteren in Anspruch genommen hätte: Vollständige, lückengefüllte Datenreihen von hoher Qualität zu erzeugen.

Wer ein hydrologisches Modell, sei es ein Wasserhaushaltsmodell, ein Niederschlagsabfluss-Modell oder eines zur Hochwasservorhersage, betreiben will, der braucht Daten zum Modellantrieb. Der Abfluss lässt sich nicht berechnen, wenn in der Niederschlagszeitreihe ein Jahr fehlt. In den allermeisten Fällen sind die Anforderungen der Modell an die Daten noch sehr viel höher: Die Modelle laufen nur, wenn die Eingangsdaten lückenlos vorliegen. Das trifft selbstverständlich nicht nur auf die genannten Modelle zu. Pflanzenwachstumsmodelle, Ökosystemmodellierung, Stadtklimamodelle und unzählige weitere mehr haben ähnliche Anforderungen. Gemessene Zeitreihen entsprechen diesen in den wenigsten Fällen: Durch mannigfaltige Ursachen kommt es zu Messausfällen, oder fehlerhafte Messungen müssen aus den Daten entfernt werden.

Verlauf der Niederschlagsdaten für Dresden Klotzsche (DWD)

Beispielhaft sei hier die Niederschlagsstation des Deutschen Wetterdienstes in Dresden-Klotzsche gezeigt, die zwischen den Jahren 1945 und 1960 keine Daten aufweist.

Um dennoch vollständige Zeitreihen zu erhalten, wird in solchen Fällen häufig auf die nächstgelegene Station mit Daten zurückgegriffen. Das führt zu inhomogenen Zeitreihen, da die umliegenden Stationen andere statistische Eigenschaften aufweisen, wie einen anderen Mittelwert, andere Extreme und verschiedene Häufigkeit von Niederschlagstagen. Es gibt weitere Verfahren, wie räumliche Interpolation, (multiple-) lineare Regression oder die Verwendung von Reanalysedaten, die alle unterschiedlich aufwendig sind und jeweils ihre eigenen Fehler haben. Für was auch immer man sich entscheidet, am Ende hat man viel Zeit in die Lückenfüllung gesteckt oder hat eine fehlerbehaftete Zeitreihe oder, im ungünstigen Fall, beides.

In meinem eigenen Fall brauchte ich für meine Arbeit Stundenwerte für Temperatur, Windgeschwindigkeit und relativer Feuchte. Im Vergleich zu Tageswerten haben Stundenwerte drei negative Eigenschaften: Die Zeitreihen sind kürzer, es gibt insgesamt deutlich weniger Zeitreihen und es gibt erheblich mehr Lücken. Außerdem kam es hier besonders darauf an, dass die lückengefüllten Daten einen möglichst kleinen Fehler aufweisen sollten. Es ging also nicht darum, ein einigermaßen befriedigendes Ergebnis zu erzielen, sondern das bestmögliche. Bei mehreren hundert Zeitreihen mit jeweils mehreren hunderttausend Zeitschritten erwiesen sich die vorhandenen Methoden als nicht umsetzbar. Einerseits war die Rechenzeit exorbitant hoch, andererseits die Qualität nicht ausreichend. Es galt also, neue Methoden zu entwickeln, die beiden Ansprüchen genügt: Einen möglichst kleinen Fehler in einer möglichst geringen Rechenzeit zu realisieren. Wie und in welchen Bereichen das gelungen ist, wird in den nächsten Blogposts erläutert.